서론
알려지지 않은 네트워크 트래픽은 보안상의 문제를 일으킬 수 있어 네트워크 상에서 오가는 패킷은 보안성 검토가 필수적
프로토콜 역공학((Protocol Reverse Engineering,PRE)
- 알려지지 않은 네트워크 프로토콜을 따르는 패킷 분석기법
- 전송되는 데이터가 사람이 읽을 수 없는 바이너리 프로토콜과 같은 다수 요인으로 인하여 전문가의 수작업에 의한 분석은 효율성 저하
-> 머신러닝 기법 이용하여 자동화 연구 활발
-> 암호통신 프로토콜 사용 비중 증가
따라서 본 연구는 구조가 비공개된 암호통신 프로토콜 패킷 구조 분석 목적, 패킷 내 바이트 단위 상관관계 분석 통해 필드 경계 파악
관련 연구
1. 암호통신 프로토콜 패킷
패킷
- 네트워크에서 데이터 전송을 위해 일정 크기로 자른 전송 단위
- 헤더, 페이로드, 트레일러로 구성
- 헤더 : 주요 제어 정보 포함
- 페이로드 : 데이터 담겨 전송
- 트레일러 : 오류 검출 등에 사용 - 각 패킷은 필드로 구분
[논문 가정]
필드 구분 위하여 동일 필드 내에 있는 바이트들은 유사한 패턴을 지니고 있다고 가정
gQUIC Q046 을 알려지지 않은 프로토콜로 가정
gQUIC Q046 : 암호통신 프로토콜 중 표준화가 진행되고 있는 QUIC(Quick UDP Internet Connections)의 특정 버전
QUIC: TCP 기반 암호통신의 지연한계를 극복하기 위하여 UDP 기반으로 개발된 HTTP(Hypertext Transfer Protocol)의 세 번째 메이저 버전
2. 암호통신 프로토콜 패킷 분석의 자동화
Chen et al. [6]
- 수작업으로 특징을 추출하고 오프라인 분석의 한계를 극복하기 위해 프레임워크 개발
- 서로 다른 애플리케이션의 정적 및 동적 행동 특성을 시계열 정보로 나타내고, 이를 RKHS(Reproducing Kernel Hilbert Space)를 이용해 다중 채널 이미지로 변환한 후 CNN(Convolutional Neural Network)을 적용
Wang et al. [7]
- 1차원 이미지 형태를 활용하여 네트워크 트래픽을 분석하는 방법을 제안
- 암호 통신 분류 과정에서 머신러닝을 사용할 때 발생할 수 있는 국부 최적해를 구하는 제약을 해결하기 위해 1차원 CNN을 활용하여 비선형 관계를 모델링
Lotfollahi et al. [8]
- 머신러닝에서 전문가의 수작업에 의존하는 매개변수 설정의 한계점을 지적
- CNN과 SAE(Stacked Auto-Encoder) 두 가지 딥러닝 기법을 사용하여 자동으로 가상 사설망(VPN)을 이용한 통신과 그렇지 않은 통신을 구별하는 Deep Packet 메커니즘을 제안
본 논문
사용자 행동 패턴에 의존하지 않고 프로토콜의 특징을 파악하기 위해 머신러닝을 활용한 암호 통신 패킷 구조 분석을 시도
제안 분석 기법
[암호통신 패킷 분석 기법 단계별 설명]
계층적 군집화 기법 - 패킷 특성 탐색 통한 프로토콜 분류 위하여 사용
피어슨 상관계수 - 순차 패턴 분석과 패킷의 바이트 간 연관성 분석하고 시각화
1. 알려지지 않은 패킷 구조 분석 절차
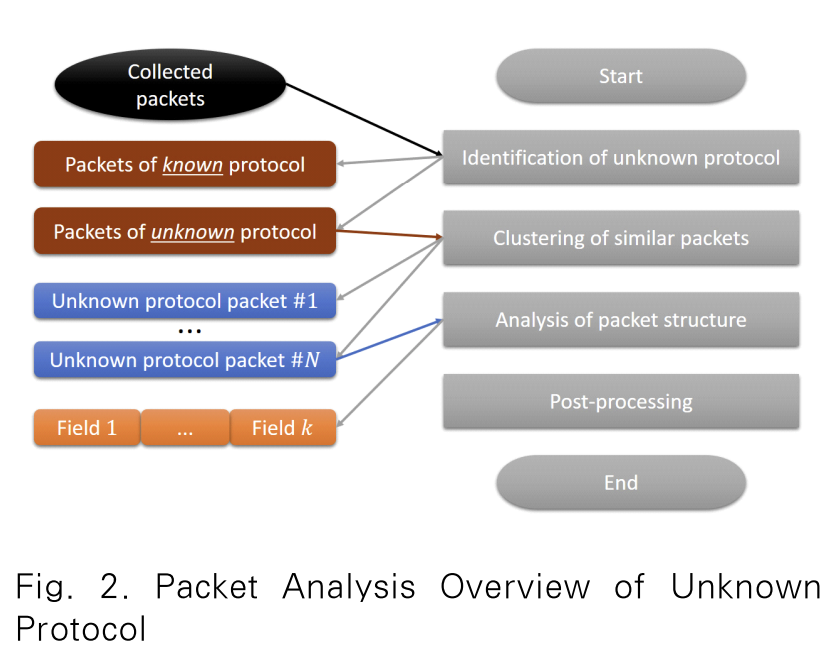
1. 프로토콜 선별
달려지지 않은 프로토콜만을 분류. 하위 계층의 헤더를 제외한 페이로드 부분만 추출
2. 유사 패킷 분류
선별 과정을 거친 패킷을 계층적 군집화 기법 적용하여 유사한 특징들을 가진 패킷끼리 묶음
3. 패킷 구조 분석
각 패킷을 구성하는 필드의 개별적인 특성을 분석하여 필드의 경계와 성질 유추
동일 구조의 패킷들은 바이트들 사이에 유사한 패턴을 나타낸다는 가정
4. 패킷 패턴 분석(후처리)
패킷의 특성별로 구분된 개별 패킷들의 흐름을 종합하여 특정 패킷이 지니는 의미 파악
2. 유사 패킷 분류
- 패킷 구조 분석의 전단계로 다른 형태의 구조를 가지는 여러 패킷 중 유사 패턴 보이는 패킷 그룹화
- 패킷에 대한 사전정보가 없는 상태에서 다른 형태의 구조를 가진 패킷들을 분류하기 위하여 계층적 군집화 기법을 적용
계층적군집화
- 상향식접근법(bottom-up approach), 비슷한 유형을 군집으로 묶어 가면서 최종 하나의 군집으로 통합될 때까지 결합하는 과정을 반복하는 알고리즘
- k-Means 군집화와 달리 사전에 군집의 수를 정할 필요가 없으므로 패킷의 필드 구조를 모르는 상황에서도 적용 용이
- 서로 다른 패킷 간의 계층적 분류는 계통도(Dendrogram)를 통하여 확인 가능. 데이터 배열의 인덱스 사이 거리는 데이터의 위치 차이를 나타내고 높이는 군집 사이의 거리를 의미
3. 패킷 구조 분석
- 패킷 내 필드를 구성하는 바이트들은 공통된 패턴을 보일 것이라는 가정하에, 순차 패턴을 사용한 패킷 내 필드 구분 시도
실험
wire shark에 의해 식별되지 않는 암호통신 패킷을 분석대상 데이터셋으로 설정
1. 데이터셋
- 표준 암호통신 프로토콜인 TLSv1.2, TLSv1.3, IETF QUIC defat-27, gQUIC Q046 암호통신 프로토콜을 따라 송수신되는 패킷을 수집하여 분석
- 국제표준화기구에 의하여 개발 중인 IETF QUIC draft-27은 WireShark에 의하여 프로토콜 식별이 가능
- Google에 의해 제안된 QUIC 프로토콜(gQUIC)의 Q046 버전은 실험 당시 WireShark에 의하여 단순 UDP 패킷으로 분류되어 암호통신 프로토콜의 식별이 정확히 이루어지지 않음
따라서 gQUIC Q046 패킷을 알려지지 않은 암호통신 패킷으로 가정하여 패킷 분류 및 구조 분석을 수행

세션 생성 초기에만 long header 패킷 수집
이후에는 데이터 송수신을 위한 short header 패킷만 수집됨

2. 프로토콜 선별
WireShark의 분석 기능을 활용한 tshark의 파이썬(Python)용 래퍼 라이브러리인 PyShark 를 이용하여 식별
- 패킷 헤더의 주요 제어 정보들을 이용하여 전송되는 데이터 종류, 형태, 패킷의 출발지 및 도착지 주소에 따라 분류하되,
알려진 프로토콜로 구분되지 않은 모든 패킷을 다음 단계의 분석 대상으로 선정
- 분류된 패킷들은 하위 계층의 헤더를 제거하여 획득한 각 패킷의 페이로드를 바이트 단위의 1차원 배열로 변환하여 이후 학습에 활용
3. 유사 패킷 분류
- 알려지지 않은 프로토콜을 따르는 패킷들을 전처리하여 1차원 배열 형태로 변환 후,
단일 연결 사용하여 계층적 군집화 적용
-좌측 노란색 군집은 long header를 가진 패킷 32개와 일치
우측 초록색 군집은 279개의 short header를 가진 패킷과 일치

4. 패킷 구조 분석
1. 순차 패턴을 이용한 구조 분석
바이트 단위 1차원 배열로 표현된 패킷의 페이 로드를 Pei et al. [10]이 제시한 PrefixSpan을 구현한 순차 패턴에 적용
순차 패턴(S sequential Pattern)
:데이터에서 시간적 또는 순서적 관계를 가진 요소들의 빈도를 분석하는 기법
Pei et al. [10]의 PrefixSpan
- 순차 패턴을 찾기 위해 설계된 기법
- 주어진 데이터에서 특정 패턴의 빈도를 효율적으로 찾아냅니다.
- 패킷의 페이로드를 이 알고리즘에 적용하여 고빈도 패턴을 추출

[Long Header 패킷 분석]
- 입력 데이터: 하위 계층의 헤더를 제거한 long header 패킷
- 고빈도 바이트 배열: `[81, 48, 52, 0, 2, 54, 80, 195]`
- 인덱스: `[0, 1, 2, 3, 4, 5, 14, 17]`
각각의 인덱스는 long header의 플래그, 버전, connection ID의 길이, 패킷 번호
[Short Header 패킷 분석]
- 입력 데이터: 하위 계층의 헤더를 제거한 short header 패킷
- 고빈도 바이트 배열: `[64, 8, 80, 97, 86, 125, 126, 128, 144]`
- 인덱스: `[0, 1, 2, 3, 4, 5, 6, 7, 8]`
각각의 인덱스는 short header의 플래그, destination connection ID, 패킷 번호
-> 고정 크기를 가지는 필드는 순차 패턴을 통해 구분할 수 있음을 보여준다
2. 피어슨 상관계수를 이용한 구조 분석
1. 피어슨 상관계수 (Pearson Correlation Coefficient)
- 두 변수 XX와 YY 간의 선형 상관관계를 계량화하는 수치로, 값의 범위는 -1에서 +1까지
+1: 완벽한 양의 선형 상관관계
0: 선형 상관관계 없음
-1: 완벽한 음의 선형 상관관계 - 피어슨 상관계수는 두 변수의 공분산과 각 변수의 표준편차를 이용하여 계산
- 는 두 변수의 공분산, σX는 변수 의 표준편차, σY는 변수 의 표준편차

패킷 분류
동일 프로토콜로 분류된 모든 패킷을 계층적 군집화(hierarchical clustering)를 통해 분석
여기서 gQUIC Q046의 long header에 속하는 430개의 패킷을 수집하고 군집화하여 상관관계를 분석
군집화 시각화
군집화의 결과로 생성된 계통도와 각 패킷의 인덱스 바이트가 속하는 군집 번호가 시각적으로 나타남
- (a): 첫 번째 바이트에 대한 군집화 결과. long header의 플래그를 나타내며 송신과 수신에 따라 값이 다르게 나타나 2개의 군집으로 분류
- (b): 두 번째에서 다섯 번째 바이트까지의 군집화 결과. gQUIC의 버전 정보가 포함되어 있어 1개의 군집으로 분류
- (c): 여섯 번째 바이트로 송수신 연결 식별 번호를 나타내며, 송신과 수신에 따라 2개의 군집으로 분류

피어슨 상관계수 계산 및 결과
- 피어슨 상관계수를 계산하기 위해 군집화된 패킷을 동일한 길이로 가공하고, 유사도가 높은 인접 바이트를 결합하여 필드 경계를 구분 바이트 인덱스를 통해 다음과 같이 필드 경계를 정의 (0, 1~4, 5, 6~13,14~16, 17, 18~)
- 상관계수 시각화: 오른쪽 그래프는 각 패킷의 인덱스를 기준으로 인접한 바이트의 유사도를 색상으로 표현
- 노란색: 유사도가 높음
- 보라색: 유사도가 낮음
- 흰색: 유사성이 없음
결과 해석
- 첫 번째 바이트는 모든 패킷에서 공통된 특징을 가지므로 유사도가 1입니다.
- 두 번째부터 네 번째 바이트는 유사성이 낮아 필드 경계로 여겨질 수 있습니다.
프로토콜 규격과의 비교
- 인덱스 14~17의 바이트는 패킷 순서를 나타내는 동일 필드로 수집된 패킷에서 통신 횟수가 적어 모두 0으로 설정된 반면, 마지막 1바이트(인덱스 17)는 값이 변경되어 다른 필드로 구분됨

결론
- 바이트 단위에서의 패킷 간 유사도를 계산하고 피어슨 상관계수를 활용 -> 필드의 경계를 높은 확률로 구분할 수 있는 가능성 확인
-이를 확장한 비트 단위에서의 분류를 통한 분류 정확도를 향상시킬 수 있을 것
- 프로토콜 역공학 기술 및 알려지지 않은 프로토콜을 대상으로 하는 공격 탐지 기술의 발전에 기여할 수 있을 것
논문 선정 이유) 정보보호학회지를 보다가 최근에 공부한 머신러닝과 관심 있던 암호 통신이 결합된 논문 제목이라 흥미로워 선정했다.
https://www-dbpia-co-kr.libproxy.swu.ac.kr/journal/articleDetail?nodeId=NODE11056767