최소 신장 트리 문제(MST; Minimum Spanning Tree)
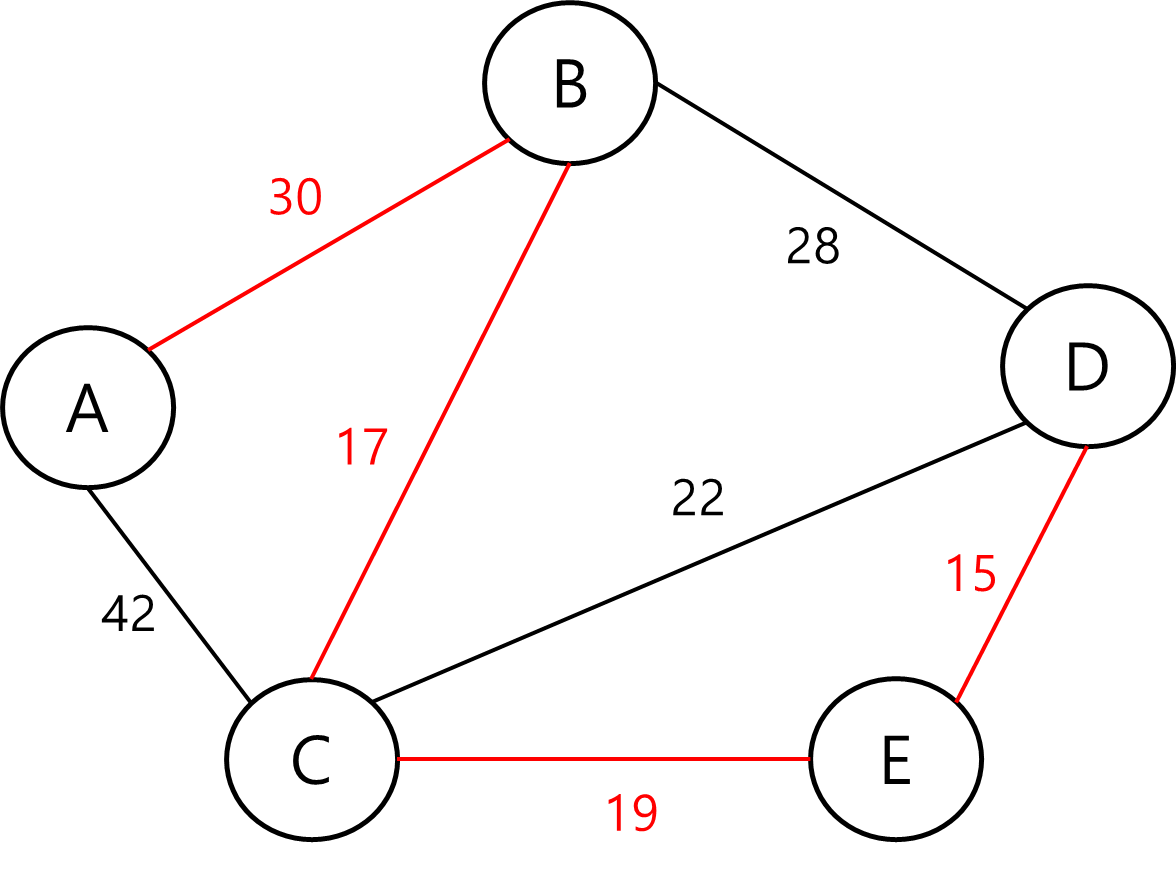
하나의 연결 성분으로 이루어진 무방향 가중치 그래프에서 간선의 가중치 합이 최소인 신장 트리
- 즉, 주어진 가중치 그래프에 존재하는 모든 정점을 연결되게끔 하는 트리 가운데, 가중치의 합이 최소
- 간선에 가중치가 있는 그래프 = 가중치 그래프
왜 트리인가?
트리 조건
- 주어진 그래프는 연결 그래프
- 주어진 그래프는 Cycle을 가지지 않음
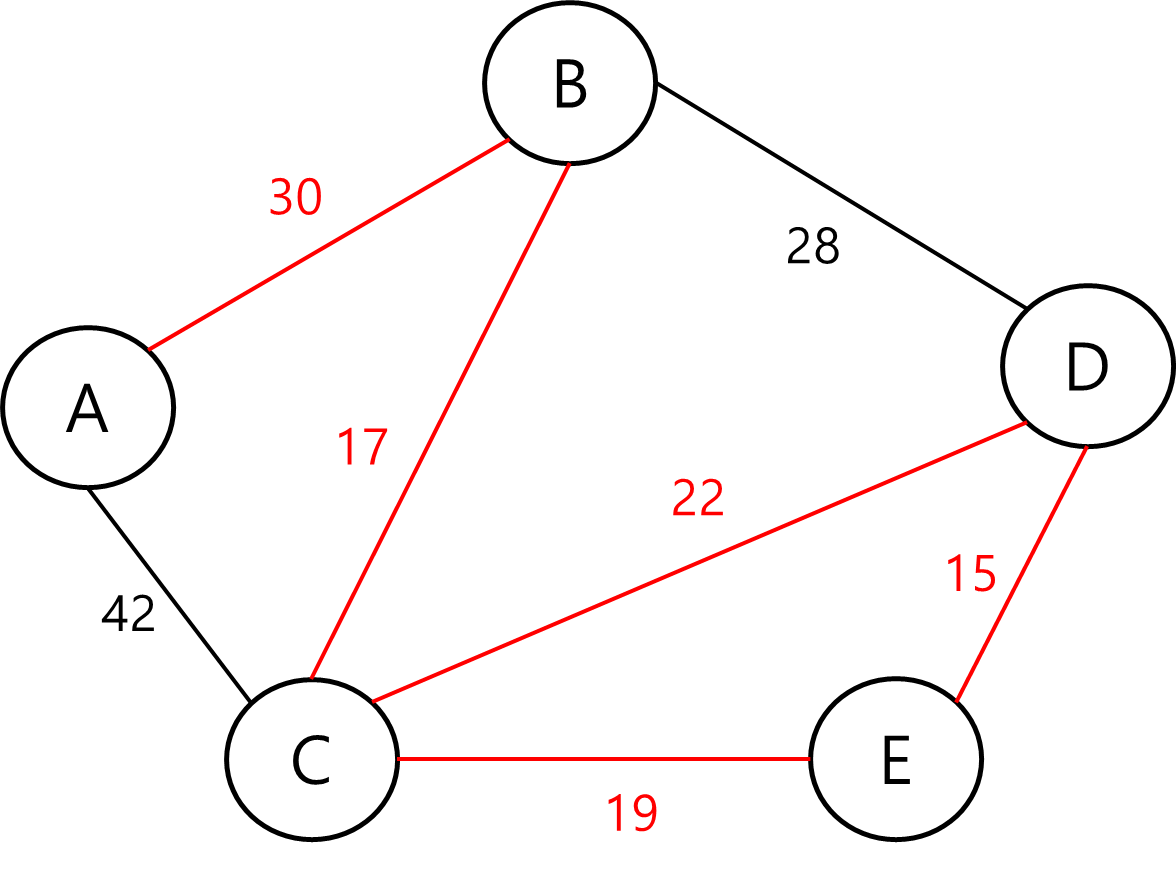
Cycle을 이루면 가중치 최소가 절대 되지 않는다.
- C, E, D로 이루어지는 Cycle에서 하나의 간선을 제외해도 각 정점은 이어짐
-> 불필요한 간선 추가되었다는 뜻
Greedy Algorithm(그리디 알고리즘)
- 최적해를 구하는 데에 사용되는 근사적인 방법
- 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것으로 선택해 나가는 방식
Prim Algorithm(프림 알고리즘)
- 임의의 정점에서 가장 적은 비용으로 이을 수 있는 정점 추가
- 만들어진 트리에서 가장 적은 비용으로 트리에 이을 수 있는 정점 선택
- 과정 반복하여 MST 생성
(접은 글) 예제
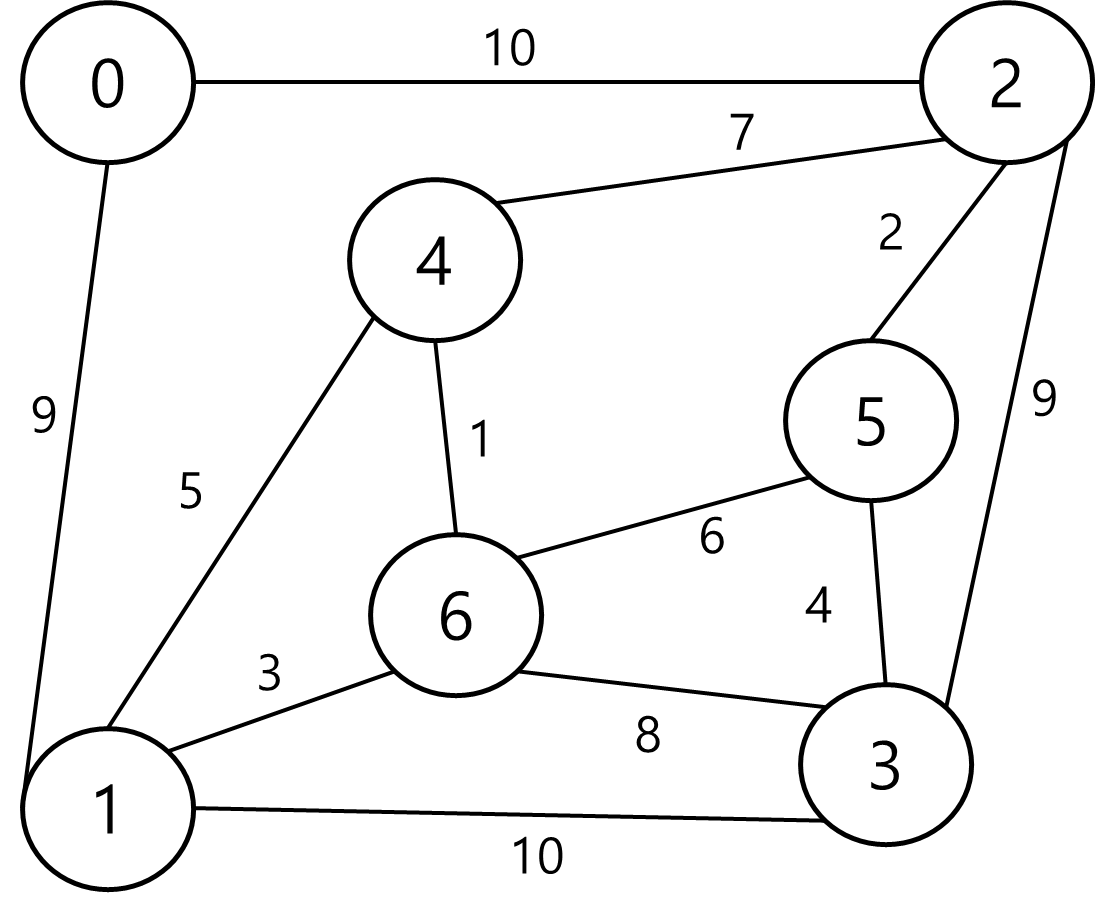
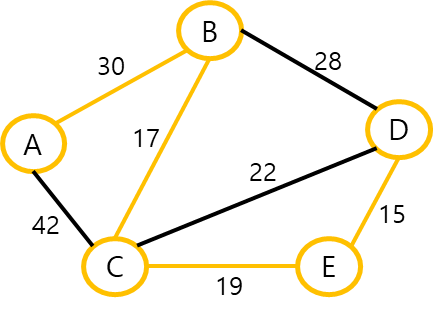
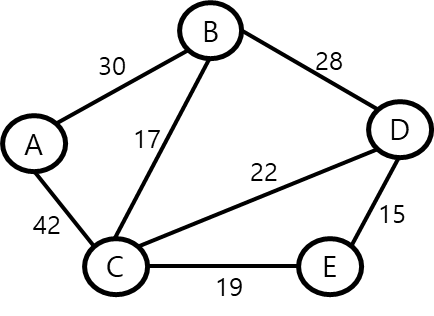
이 가중 그래프에서 최소 비용 신장 트리를 구성했을 때,
가중치의 합을 구해보자.
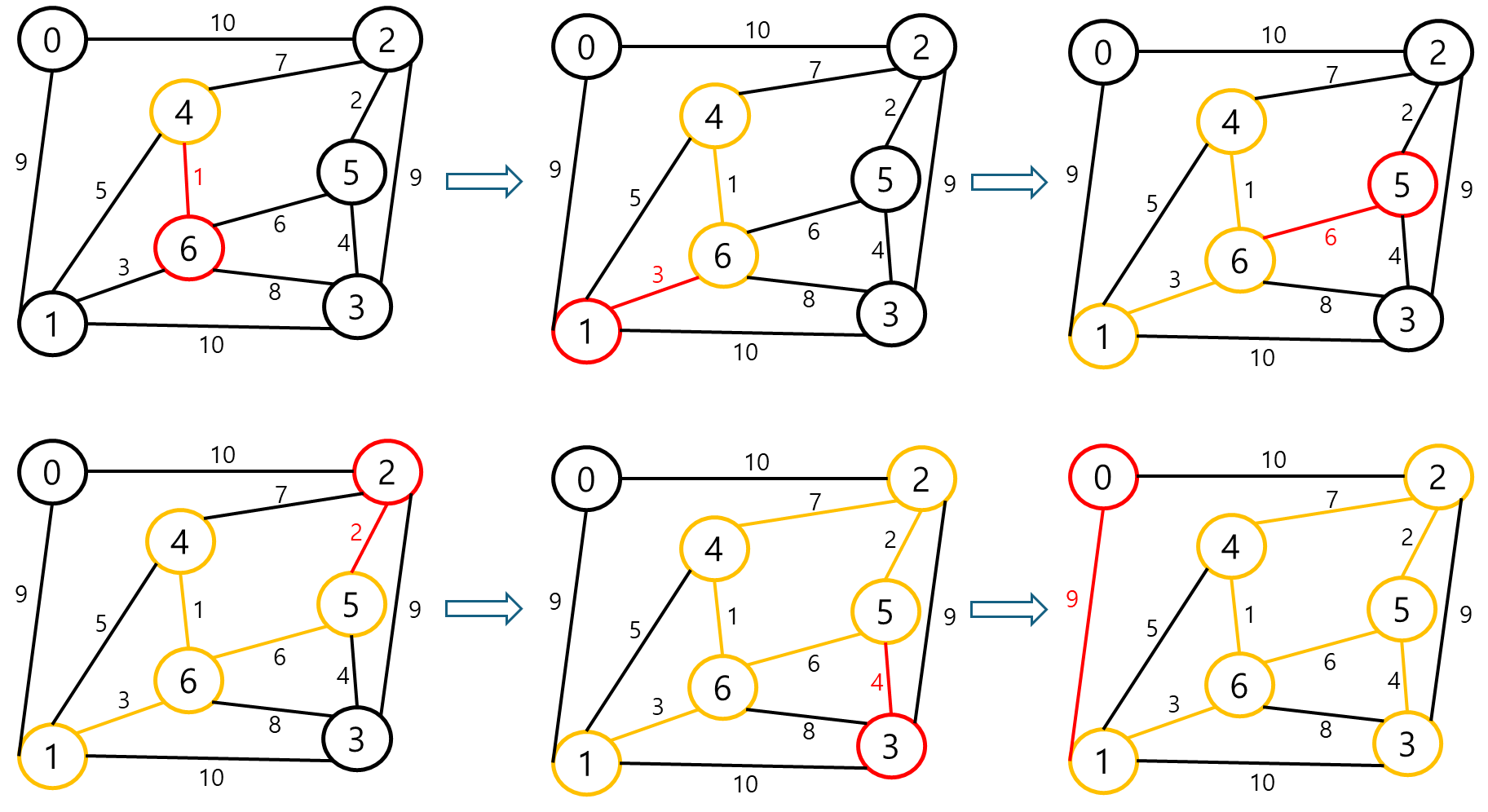
- 4를 임의의 정점으로 잡았다. 가장 적은 비용(1)으로 이을 수 있는 6을 추가한다.
- 4와 6으로 이어진 트리에서 가장 적은 비용(3)으로 이을 수 있는 정점 1을 추가한다.
- 4,6,1로 이어진 트리에서 가장 적은 비용(6)로 이을 수 있는 정점 5를 추가한다.
- 4,6,1,5로 이어진 트리에서 가장 적은 비용(2)로 이을 수 있는 정점 2를 추가한다.
- 4,6,1,5,2로 이어진 트리에서 가장 적은 비용(4)로 이을 수 있는 정점 3을 추가한다.
- 4,6,1,5,2,3으로 이어진 트리에서 가장 적은 비용(9)로 이을 수 있는 정점 0을 추가한다.
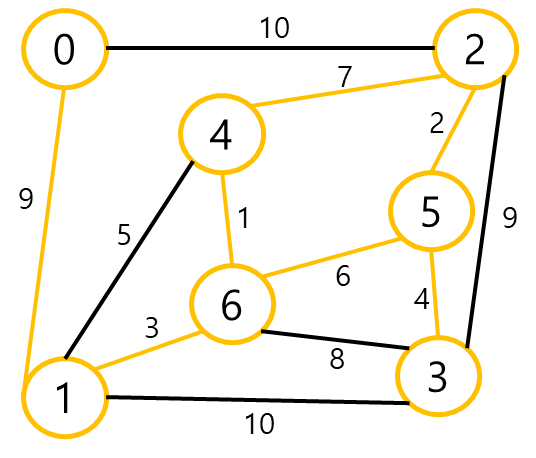
따라서, 가중치의 합은 1+3+6+2+4+9 = 25이다.
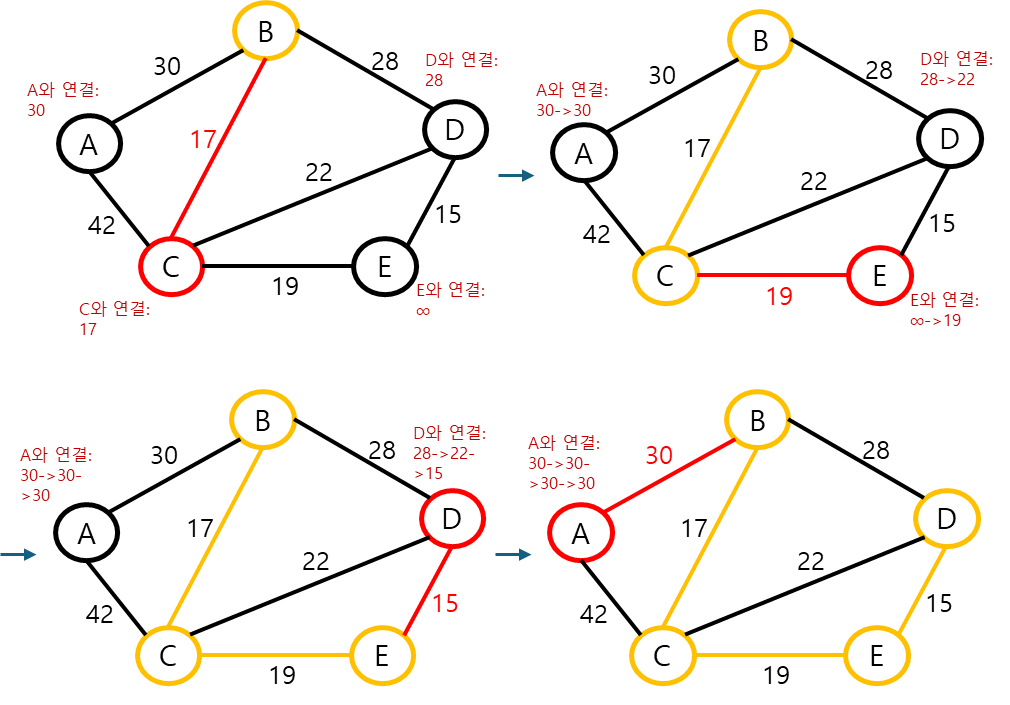
Prim Algorithm 구현
- 아직 연결되지 않은 노드들에 대해서 연결 비용 업데이트
- 그 중 최솟값 취함
(접은 글) 예제
Prim Algorithm 시간복잡도
O(2(V-1) * V) = O(V^2)
정점의 개수를 V라고 가정.
1. 하나의 임의의 정점을 고르고, 이와 연결되지 않은 정점들과의 가중치 업데이트 : V-1번 수행
2. 그 중 최솟값 찾기 : V-1번 비교 수행
3. 위 과정 모든 정점 V에 대해 수행
Prim Algorithm 성능 향상
-> 우선순위 큐 이용하여 데이터 추가하면서 계속 최솟값 찾기
우선 순위 큐(Priority Queue)
- 들어온 순서와 무관하게 우선 순위가 높은 원소부터 나감
- 맥스힙을 이용하여 구현
- 힙에서 데이터 추가 및 루트 노드 삭제 시, O(logN)의 시간복잡도를 가짐
- 따라서, 힙 이용하여 우선 순위 큐 구현하면 빠르게 수행 가능
우선 순위 큐를 이용한 후 총 시간복잡도 (간선의 수는 E, 정점의 개수는 V)
O(ElogE + ElogE) = O(2ElogE)
이 때, 간선의 수는 최대 V(V-1)/2개
즉, E <= V^2
따라서, O(ElogV^2) = O(2ElogV) = O(ElogV)
-> 개선됨
그러나.. 모든 간선이 다 연결되어 있으면 O(V^2logV)이므로 성능 더 나빠짐...
그치만... 모든 간선이 다 연결되어 있을 경우가 적기 때문에 성능이 좋아졌다고 하는거
접은 글 참고
큐를 이용한 후 성능 향상
1. heappush 한 번 할 때의 시간복잡도는?
**N개의 원소가 있을 때의 맥스힙의 시간복잡도: O(logN)
힙에는 최대 E개만큼 들어갈 수 있음 (즉, E개의 원소)
따라서 heappush의 시간복잡도는 O(logE)
2. (OlogE)의 시간복잡도를 가진 heappush를 E번 수행
따라서 heappush연산은 총 O(logE)만큼의 시간복잡도

heap에서 pop하면서 정점 연결 시에도 간선의 개수 E만큼 heappop 수행
1. heappop 한 번 할 때의 시간복잡도는
O(logE)
2. O(logE)의 시간복잡도를 가진 heappop을 E번 수행
따라서 heappop연산은 총 O(ElogE)만큼의 시간복잡도
Prim Algorithm 구현
- 큐 이용
from heapq import heappush, heappop
G = [[0, 30, 42, 0, 0],
[30, 0, 17, 28, 0],
[42, 17, 0, 22, 19],
[0, 28, 22, 0, 15],
[0, 0, 19, 15, 0]]
V = ["A", "B", "C", "D", "E"]def Prim_Algorithm(graph, graph_v, start):
h = list() #힙 정의
connect = list()
for i in range(0, len(graph)):
connect.append(False) #각 정점이 연결되었냐, 안 되었냐 표시,
heappush(h, (0,start)) #힙 h에 (0,start)를 push (start 연결하는데 비용 0)
total_weight = 0 #가중치 합 저장
vertex_count = 0 #정점이 모두 포함되면 끝이므로 개수 세기 위해 필요
while vertex_count < len(graph): #정점 모두 포함되기 전까지 while문 반복
pop_info = heappop(h) #가장 우선순위에 있는 데이터를 pop(가중치의 최솟값 반환)
pop_weight = pop_info[0]
pop_vertex = pop_info[1] #pop한 노드 정보 저장
if connect[pop_vertex] == False:
connect[pop_vertex] = True #pop한 노드 연결 안 되어있으면(False) 연결(True)
total_weight = total_weight + pop_weight
vertex_count = vertex_count + 1 #가중치 합에 추가하고, 정점 수에도 하나 추가
print('새로 연결된 곳:', graph_v[pop_vertex])
print('누적 가중치 합:', total_weight)
for i in range(0, len(graph)): #아직 연결되지 않은 노드들에 대해서 연결 비용 업데이트
if (graph[pop_vertex][i] != 0) and (connect[i] == False): #그래프 내 i번째 정점과 pop한 정잠과 연결되어 있고, 아직 연결되지 않았다면
heappush(h, (graph[pop_vertex][i], i)) #(해당 가중치, 해당 정점)을 push
ex)

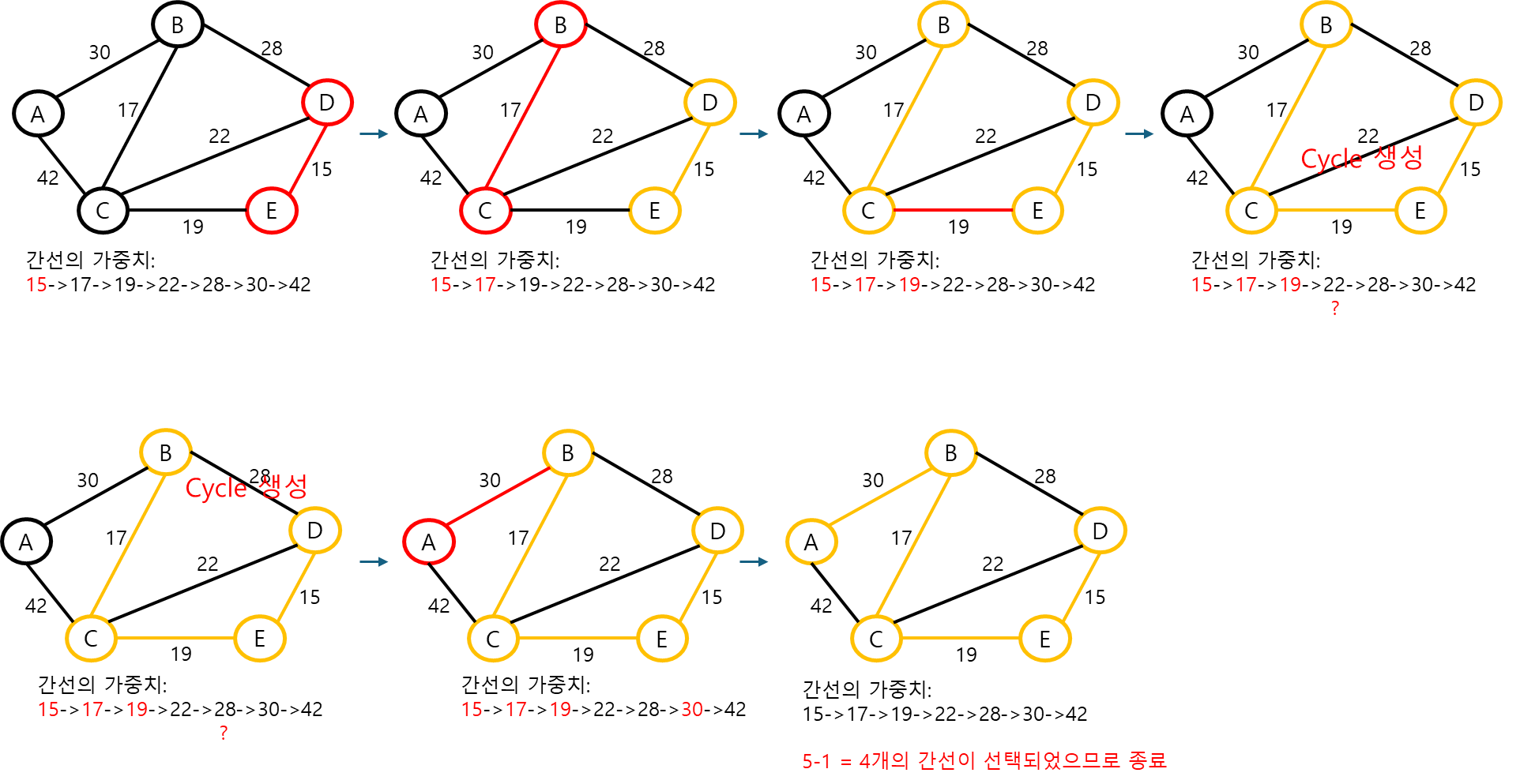
Kruskal Algorithm(크루스칼 알고리즘)
- 그래프에 존재하는 모든 간선들을 가중치 순으로 나열
- 그래프 내 정점이 모두 이어질 때까지 가중치가 낮은 간선 순서로 선택
-
- 가장 가중치가 작은 간선을 트리에 추가하여 사이클을 만들지 않으면 트리 간선으로 선택
- 사이클을 만들면 버리는 것을 반복
- n-1개의 간선이 선택되면 알고리즘 종료
Kruskal Algorithm 구현
- 가중치 순서로 나열 -> sort() 함수 이용
- cycle 형성 여부 어떻게 판단?
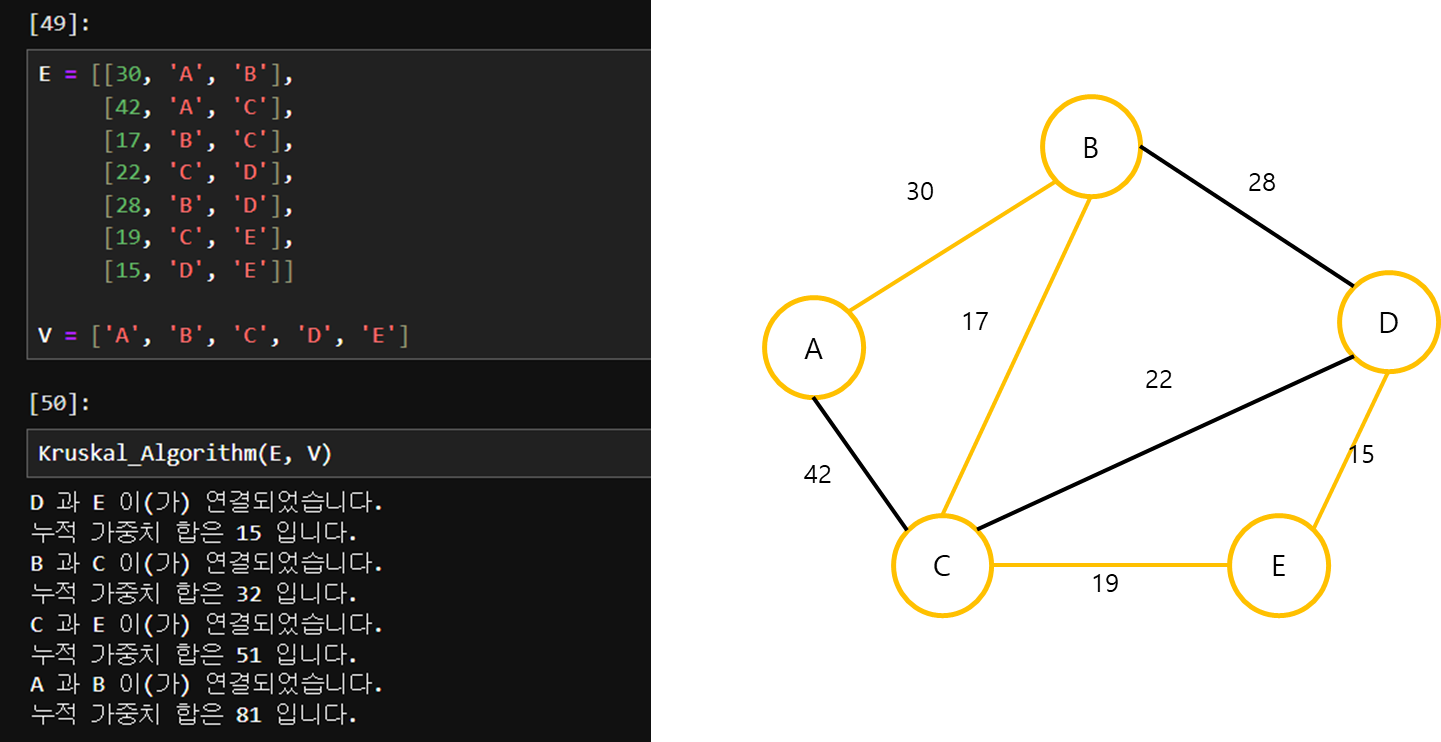
def Kruskal_Algorithm(edges, vertexes):
edge_count = 0 #이어진 간선의 수 세기 (간선의 수가 정점 -1개이면 break)
total_weight = 0 #최종 가중치
union = dict() #딕셔너리 이용해서 집합 표기
for each_vertex in vertexes:
union[each_vertex] = each_vertex #초기값 셋팅 dict = {'A':'A','B':'B','C':'C','D':'D','E':'E'}
edges.sort() #간선의 가중치 오름차순 순으로 정렬 O(ElogE) = O(ElogV)
for each_edge in edges: #정렬된 edges 차례로 돌기
if union[each_edge[1]] != union[each_edge[2]]: #each_edge 형태 = [weight, node1, node2] (node1과 node2가 같은 value 값을 가지는가?
total_weight = total_weight + each_edge[0]
edge_count = edge_count + 1 #같은 집합에 없으면 잇기. 최종 가중치에 추가, edge_count에도 1 추가
print(each_edge[1], '과', each_edge[2], '이(가) 연결되었습니다.')
print('누적 가중치 합은', total_weight, '입니다.')
for each_vertex in vertexes:
if union[each_vertex] == union[each_edge[2]]:
union[each_vertex] = union[each_edge[1]] #간선을 연결했으므로 정점들은 같은 집합이 됨. 해당 정점들의 value 값 일치시키기
if edge_count >= len(vertexes) - 1:
break #연결한 간선의 수가 정점의 수 -1 이면 break
ex)